A
K LEO ABOUT
THERMO
Cascaded Carnot Cycle Heat Engines
Q. I need your help with a question as follows:
Two reversible heat engines operate in series between a source at 527°C and sink at 17°C. Assuming that each engine operates on the Carnot cycle, if the engines have equal efficiencies and the first rejects 400 kJ to the second what is:
1. the temperature at which the heat is supplied to the second engine?
2. the heat taken from the source?
3. the work done by each engine?
I would welcome any pointers you can offer.
R. In thermodynamics the concept of reversible heat engines being cascaded (such that the heat sink of one engine is the source of the next engine) in the way you have described is a very important one: it is closely connected with the definition of temperature scales. If you really want to have a good grasp of this problem you should look up a thermodynamics textbook about how the absolute temperature scale is defined in terms of the heat transfer amounts of a reversible heat engine.
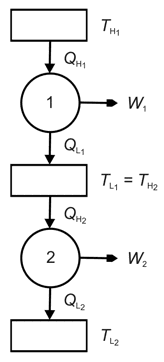
The figure below shows two engines where the heat sink of engine 1 is the heat source of engine 2. In fact, the two reversible heat engines taken together are fully equivalent to one single reversible heat engine that accepts heat transfer 
at temperature 
and rejects heat transfer 
at at temperature 
while providing a net work output of 
.
The thermal efficiency of a Carnot cycle engine is given by
where 
and 
are the absolute temperatures of the heat source and heat sink respectively and where 
and 
are the amounts of heat transfer to and from the engine. The equivalence between the heat transfer ratio 
and the ratio of absolute temperatures 
comes from the way the absolute temperature scale is defined. It always applies for a reversible heat engine operating between two fixed-temperature reservoirs.
Hence
(1)
Coming back to your problem, the two reversible engines have equal efficiencies, so
and hence
, but 
and so
, or 
and so
(2)
Equation 2, which only applies when the thermal efficiencies of the two heat engines are equal, can be used to find the temperature of the common, intermediate, thermal reservoir.
Applying equation 1 to engine 1
(3)
Equation 3 can be used to find the heat input when the heat rejection and the temperatures of the thermal reservoirs are known.
There are various ways in which you could go about calculating the net work outputs 
and 
using the expressions already mentioned above. Once you have found the temperature of the intermediate thermal reservoir, and as the temperatures of the other two reservoirs are given, you can calculate ther thermal efficiency, which is the same for both heat engines. Once you have found the heat transfer to the first heat engine and as the heat transfer to the second heat engine is given, you can multiply each heat input amount by the thermal efficiency to find the work output of the engine.
Alternatively you could find the work quantities as the difference between the heat input and the heat rejection of each engine. For the second engine the heat rejection could be calculated from the heat input using equation 1, applied to that heat engine.
The temperatures in the expressions are all absolute temperatures, so don't forget to convert the Celsius values to Kelvin (0°C corresponds to 273.15 K).
From equation 2
From equation 3
