AK LEO ABOUT THERMO

Non Steady Flow Energy Equation

Q. I have a heat transfer problem, which was raised by a group of students. The problem is concerned with the design of a cooling reservoir that is part of their final year project. Basically, they asked me how to calculate the temperature at time, t, of the water in a reservoir. The reservoir receives a constant water supply, say, 100 m^3/hour at a temperature of, say, 45 C. The reservoir has an initial volume of water, for example, 100 m^3 at a temperature, say 10 C. If we assume that the reservoir has a size of 1m x 30m x 30m (water exposed area is 900 m^2), about 8 hours are required to fill the reservoir and then the excess of water will be over flown. The problem is how to estimate the water temperature, Tt, at a time, t. In other words, to check the time required for the water in the reservoir, to cool down to the ambient temperate (8 C). I would be very grateful if you can help me with this problem. Kind regards.

R. This problem is an example of a non steady open system. Let the system boundary enclose only the water that is inside the reservoir. The underlying principle is that the net rate at which energy is transferred and transported into the system equals the rate of change of the energy of the system.

Internal energy is transported into and out of the system with the water flows and is lost from the system as heat transfer to the surroundings. When the relevant simplifying assumptions are made the situation is described by a first order differential equation in temperature. This can be integrated from the initial temperature of the water in the reservoir at time zero to give the temperature of the water at any future time. The flow rate of water into the system is steady. There is no flow out of the system until the overflow level is reached. Thereafter the flow rate out of the system is steady and equals the flow rate in. After a finite time the temperature of the water leaving will be within a specified tolerance of the eventual (infinite time) steady state value.

You may or may not agree with the simplifying assumptions mentioned here. They are your responsibility and you can adapt them as appropriate.

The water can be regarded as an incompressible liquid.
The specific heat of the water can be taken as constant.
Kinetic energy of the water streams and the water in the reservoir can be neglected.
Potential energy changes can also be neglected; they have no influence on the temperatures in this problem.
Flow work terms (commonly dealt with by the use of the enthalpy property to include both flow work transfer and internal energy transport) and displacement work terms associated with the change in volume of the system boundary cancel out and do not affect the temperatures.
A reservoir such as this may be subject to stratification and significant temperature variations may exist within it. For analysis purposes complete and continuous mixing of the water in the reservoir (without fluid friction) will be assumed.
As a consequence of the ongoing mixing, the temperature of the water coming out of the reservoir is equal to the temperature of the water in the reservoir.
From the mass balance point of view the loss of water from the surface can be neglected. However, the evaporative effect at the surface will be significant in energy terms (unless the air above the surface is saturated). It is common practice to deal with this as heat transfer between the water surface and the air.
The rate of heat transfer from the water in the reservoir to the surroundings can be described and evaluated in terms of the temperature of the water, the temperature of the surroundings and the water level (if there is heat transfer through the side walls of the reservoir).

The non flow energy equation for the system can be written as follows:

Non steady flow energy equation

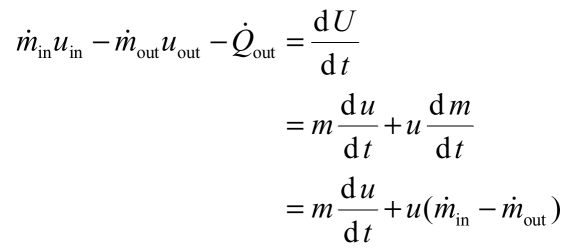
The following expressions describe the specific internal energy of the water, the rate of heat transfer out of the system to the surroundings and the mass of water in the system:

Internal energy, heat transfer rate, mass

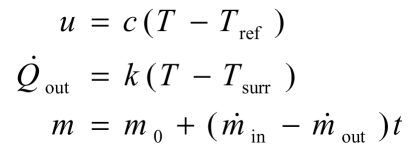
The differential equation describing the rate of change of the temperature reduces to:

Differential equation in temperature

Symbols
T Temperature t Time m Mass U Internal energy u Specific internal energy		Q Heat transfer c Specific heat capacity k Heat transfer coefficient surr Surroundings ref Reference zero state for u

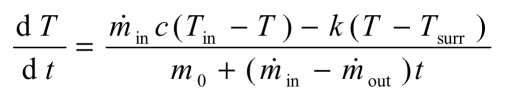
Leo Nest, ULFC

<< Back to Ask Leo About Thermo

Send questions or comments about this site to Webmaster.

Fun-Engineering.net